流体流动的基本原理是化工原理课程的重要基础,因其不仅是流体输送、搅拌、沉降及过滤的理论基础,也是传热与传质过程中各单元操作的理论基础。而伯努利方程及其应用是流体流动zui核心的内容,因此,掌握伯努利方程及其应用对于学好化工原理课程极为重要。
在化工原理课程的教学实践中,伯努利方程及其应用一直被认为是贯穿整个教学过程的重点和难点。关于对伯努利方程的理解已有很多文献报道,本文在此不过多介绍。为了帮助学生更好地掌握伯努利方程应用,本文针对学生在学习中可能会遇到关于伯努利方程应用的问题,对其进行系统的讨论分析,希望对学习者有所帮助。
1、伯努利方程
伯努利方程描述的是理想流体流动过程中机械能守恒的问题,其中不存在机械能损失,只涉及流体动能、位能和静压能之间的相互转换。但化工生产中很多流体都是实际流体,其流动过程中一部分机械能因内摩擦力而转化为内能,使得流体流动过程机械能不守恒。为保证流体的稳定连续流动,通常采用泵做功的方式向流体补充相应的机械能,其衡算关系为: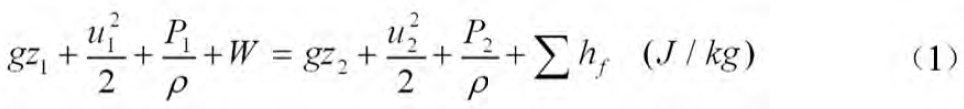
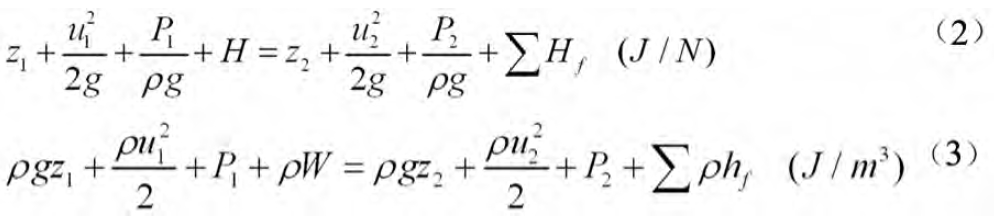
式( 1) 、( 2) 和( 3) 均为实际流体机械能衡算式,习惯上也称为实际流体的伯努利方程式( 下文中伯努利方程均指实际流体的伯努利方程) 。3 个衡算式只是能量衡算基准不同,分别对应单位质量流体、单位重量流体和单位体积流体,应用时可以灵活选择。
在伯努利方程应用中,需特别注意其适用范围,即稳定流动下的不可压缩流体。这是很多同学在应用伯努利方程解题时zui容易忽视的地方,往往不加任何判断选取两个截面直接就列衡算方程。一般条件下的液体可认为是不可压缩性流体,但若所处理的流体为气体时,必须先判断伯努利方程是否适用。若两衡算截面间的压力变化不超过20%,方可用于工程应用上的近似计算,并且方程式中的密度ρ 应取两截面间平均压力下的平均值。此外,还需要特别注意方程式中的压力P1、P2,除了要求两者单位统一外,还必须要求其表达方式也一样,即同为绝压,或同为表压。
2、伯努利方程的应用
伯努利方程是流体流动的基本方程式,其应用范围很广,可用于确定设备间的相对位置、流体流量、输送机械的有效功率等。下面根据单位质量流体的伯努利方程,就习题中可能会遇到的问题,将其应用分为基本应用和扩展应用分别加以讨论,如图1 所示。

图1 伯努利方程应用示意图
2.1 基本应用
2.1.1 确定设备间的相对位置ΔZ
ΔZ可用于确定为达某种流体输送目的,两设备需满足的相对位置。此类问题在习题中通常以求解高位槽液面高度的形式出现。根据题意,确定方程式中其他各项的值,即可解出ΔZ。
2.1.2 确定管道中流体的流量qv
伯努利方程中的u 为流体在管中的平均流速,结合连续性方程( qm=ρAu 或qV=Au) ,即可确定管道中流体流量。
2.1.3 计算管路中各点的压力P或压力差ΔP
通过在管路中某点所在截面A 与某已知压力截面B 之间列伯努利方程,即可确定某点的压力。或通过在管路中任意两截面间列伯努利方程来确定两截面间的压力差。
2.1.4 确定输送机械的有效功率及轴功率
方程中W指单位质量流体从流体输送泵处获得的有效机械能,将W值乘以质量流量即为输送机械的有效功率Ne,再除以泵的效率即为所需泵的轴功率N。根据N 或Ne值可以选择合适的输送机械。
2.1.5 确定管路中流体的流动方向
管路中流体的总机械能ΔE 为流体的位能、动能和静压能之和。流体在管路中流动时,因存在阻力,其流动方向总是沿着机械能降低的方向。因此,通过计算两截面上的总机械能,可以判断流体流动方向。
2.1.6 确定阻力损失
方程中Σhf为两衡算截面间的总阻力损失,包括直管阻力和局部阻力。通过伯努利方程,可以确定管路中某段管路的阻力损失。此外,管路中流体流动阻力还可以通过阻力公式直接计算获得。
2.2 扩展应用
2.2.1 流量测量
与静力学基本方程联用,用于管路中流体流量的测量。化工生产中常用的流量计( 包括测速管、孔板流量计、文丘里管流量计、转子流量计等) 都是利用流体流动过程中机械能转化原理而设计的。例如,孔板流量计就是利用流体流经孔板时,静压能转换为动能,产生压力差,再通过测量此压力差来实现流量的测量。
2.2.2 管路计算
管路计算就是综合运用伯努利方程、连续性方程、摩擦阻力损失计算式、摩擦系数计算式等解决实际生产中常遇到的管路系统的设计和操作问题。管路系统可分成简单管路和复杂管路,这里只讨论简单管路。简单管路包括等径管和串联管,常遇到的管路计算问题主要包括以下三种。
①摩擦阻力损失Σhf的计算( 已知l、d、ε/d、qv( 或u) ,求Σhf) ,这类计算相对简单,先根据u 计算出Re,再根据Re 和ε/d计算或查图求出λ,zui后根据阻力计算公式解出Σhf即可。
②流量计算( 已知l、d、ε/d、Σhf,求qv( 或u) ) ,为避免试差计算,可以将阻力公式和Re 计算式代入λ 的经验计算式,如布拉修斯( Blasius) 关联式、考莱布鲁克( Colebrook) 关联式以及哈兰德( Haaland) 关联式等,解出流速u。需特别注意的是解出流速u 后,需要验算所采用经验公式的适用条件是否满足。
③管径计算( 已知l、Σhf、ε、qv,求d) ,这类问题较复杂,因Re = duρ /μ 与ε /d 中都有d,需要用试差法计算。首先根据题意,找出λ 和d 的关系式,即试差等式,然后按照图2 所示方法进行试差,计算出所需管径。在实际应用中,应根据具体的设计需要,选用总费用( 包括动力费和设备费) zui省的管径,即适宜管径。
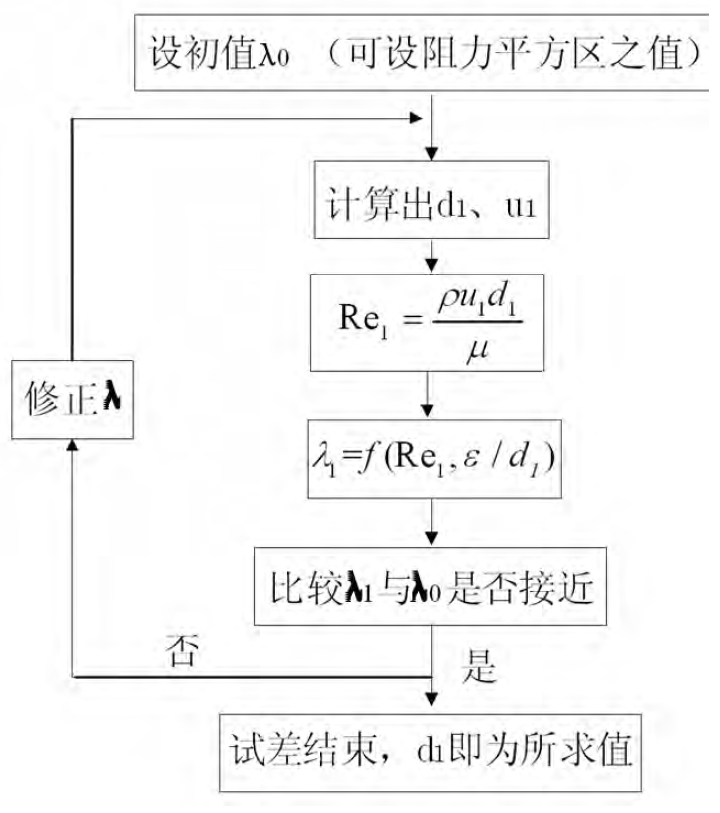
图2 试差过程示意图
电话
微信扫一扫
